1.2.2 期待値と分散

期待値

• $E\left[f\right]={\sum }_{x}p\left(x\right)f\left(x\right)$

• $E\left[f\right]=\int p\left(x\right)f\left(x\right)dx$

• $E\left[f\right]\simeq \frac{1}{N}{\sum }_{n=1}^{N}f\left(x_n\right)$

  • 離散・連続を問わず有限の$N$点で近似可能
  • $N\to \infty$ の極限で厳密になる。
  • サンプリング（11章）などで用いる

多変数の場合、平均を取る変数を指定する

$E_x\left[f\right(x,y\left)\right]$

この場合、 $x$ について周辺化されており、結果は $y$ についての関数になる。

条件付き期待値

• $E_x\left[f|y\right]={\sum }_{x}p\left(x|y\right)f\left(x\right)$

  • 条件付き確率に事前条件が反映されるだけ

• 連続変数についても同様

分散

• $var\left[f\right]=E\left[\right(f\left(x\right)-E\left[f\right(x\left)\right]{)}^2]$

  • $f\left(x\right)$ がその平均値 $E\left[f\right(x\left)\right]$ の周りでどれだけばらつくか、を表す

• $var\left(x\right)=E\left[\right(x-E\left[x\right]{)}^2]$

  • 確率変数 $x$ についても分散を考えたもの
  • 恒等関数をとるのと同義

独立であれば共分散は0

• 直感的には、

  • 独立 $\iff$ 『同時に変動する度合い』が0

• $E_{x,y}\left[xy\right]=E\left[x\right]E\left[y\right]$ を示せば良い

  • → 次ページ

1.2.3 ベイズ確率

ベイズ vs 頻度主義

• 頻度主義的・古典的確率
  • 確率は、ランダムな繰り返し試行の頻度
• ベイズ的確率
  • 確率は不確実性の度合い
  • 事前分布という信念を導入する
• どこまで主観性を認めるかが違い
• PRMLでは、有用な場面ではどちらも用いる（ベイズ多め）

ベイズ確率を採用する根拠

• 確率の加法・乗法定理（ベイズの定理）が、信念の定量化・操作のための単純な公理集合から導かれる (Cox, 1946)
  • 確率論 $\equiv$ ブール論理を不確実性を含む場合に拡張したもの (Jaynes, 2003)
• その他にも多くの提案されている性質や公理が、確率の乗法・加法定理に従う

ベイズ確率

$p\left(w|D\right)=\frac{p\left(D|w\right)p\left(w\right)}{p\left(D\right)}$

事後確率 $\propto$ 尤度 $\left(p\right(D|w\left)\right)\times$ 事前確率

• データを観測する前に$w$に関する仮説を事前分布$p\left(w\right)$として表現できる
• $D$というデータを得た 事後 の、$w$の不確実性を評価できる

ベイズ確率

$p\left(D\right)=\int p\left(D|w\right)p\left(w\right)dw$

• 尤度$\left(p\right(D|w\left)\right)$は確率分布ではない（積分は1になるとは限らない）
• $p\left(D\right)$は、事後確率$p\left(w|D\right)$を確率分布にするための定数
• 事後確率$p\left(w|D\right)$、 尤度$p\left(D|w\right)$、事前確率$p\left(w\right)$はすべて$w$の関数となっている

尤度関数

• ベイズ・頻度主義どちらでも重要となる
• ベイズでは
  • データ$D$のみがあり、 $w$は確率分布
• 頻度主義では
  • $w$は固定パラメータ、推定量として
  • データ$D$の分布を考慮して得る（最尤推定）

事前分布

• 頻度主義では、コイン投げで3回連続で表が出ると、表が出る確率は100％になる
• ベイズ確率で、事前分布を導入すれば、それほど極端な値にはならない
  • 逆に言えば、悪い事前分布を選べば高確率で悪い結果になる
    • この場合、頻度主義では、交差確認（1.3節）を使える

ベイズの計算コスト

• モデル選択や予測に必要な 周辺尤度（エビデンス） $p\left(D\right)$ の計算が重い
  • $p\left(D\right)={\sum }_{w}p\left(D|w\right)p\left(w\right)$
  • 離散の場合は組み合わせ爆発
  • 連続の場合には積分が解析不可能
    • ガウス分布等であれば解析も可能
  • MCMC（サンプリング法, 11章）や計算機の発達により実用的に
  • 変分ベイズやEP法（期待値伝播法）等の決定論的近似法（10章）も寄与

1.2.4 ガウス分布

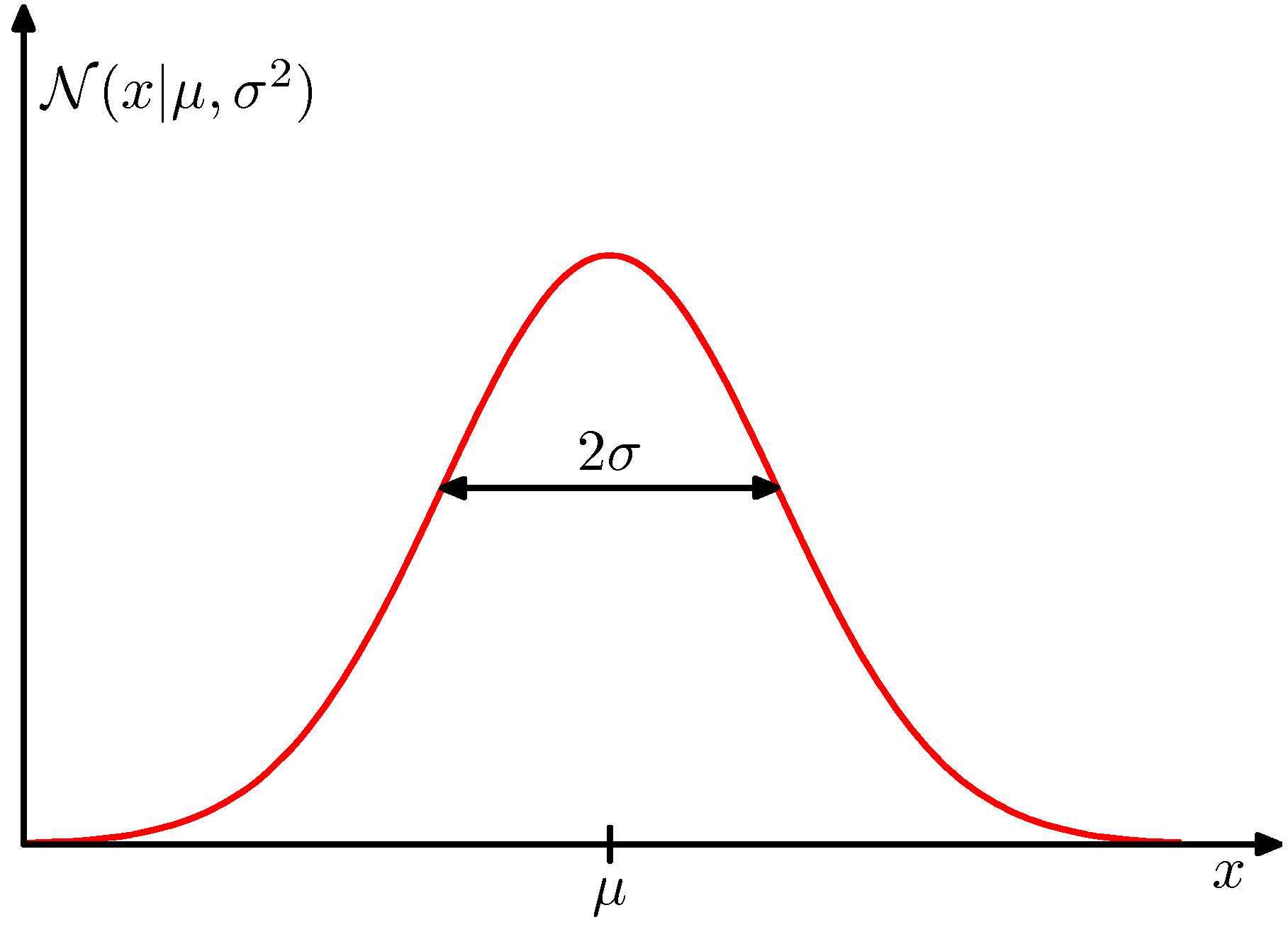
ガウス分布

$N(x|\mu ,{\sigma }^2)=\frac{1}{(2\pi {\sigma }^2{)}^{1/2}}\exp \{-\frac{1}{2{\sigma }^2}(x-\mu {)}^2\}$

• $\beta =1/{\sigma }^2$ を精度パラメータという
• 確率密度である
  • $N(x|\mu ,{\sigma }^2)>0$
  • $\int N(x|\mu ,{\sigma }^2)dx=1$

ガウス分布

• 期待値・平均値 $\mu$
• 2次モーメント $E\left[x^2\right]=\int N(x|\mu ,{\sigma }^2)x^{2}dx={\mu }^2+{\sigma }^2$
• よって分散は $var\left[x\right]=E\left[x^2\right]-E[x{]}^2={\sigma }^2$
• 最頻値は平均値に一致

多変量正規分布

$N(x|\mu ,\sum )=\frac{1}{(2\pi {)}^{D/2}}\frac{1}{(|\sum |{)}^{1/2}}\exp \{-\frac{1}{2}(x-\mu {)}^T{\sum }^{-1}(x-\mu )\}$

• 多変数にしたもの
• $\sum$は共分散
• $|\sum |$は共分散の行列式
• 詳細は2.3節

ガウス分布のパラメータ推定

• N個のデータ点が同じガウス分布から独立に生成されるとする
• データ点が同じ分布から独立に生成されることを、 独立同分布(i.i.d.) という
  • independent identically distributed
• パラメータ$\mu ,{\sigma }^2$を求めたい

ガウス分布に対する尤度関数

$p(x|\mu ,{\sigma }^w)={\prod }_{n=1}^{N}N(x_n|\mu ,{\sigma }^2)$

• 独立な確率変数集合の同時分布なので、積をとればよい
• 与えられたデータの同時確率を最大化するパラメータを求めれば良い

ガウス分布に対する尤度関数の図示

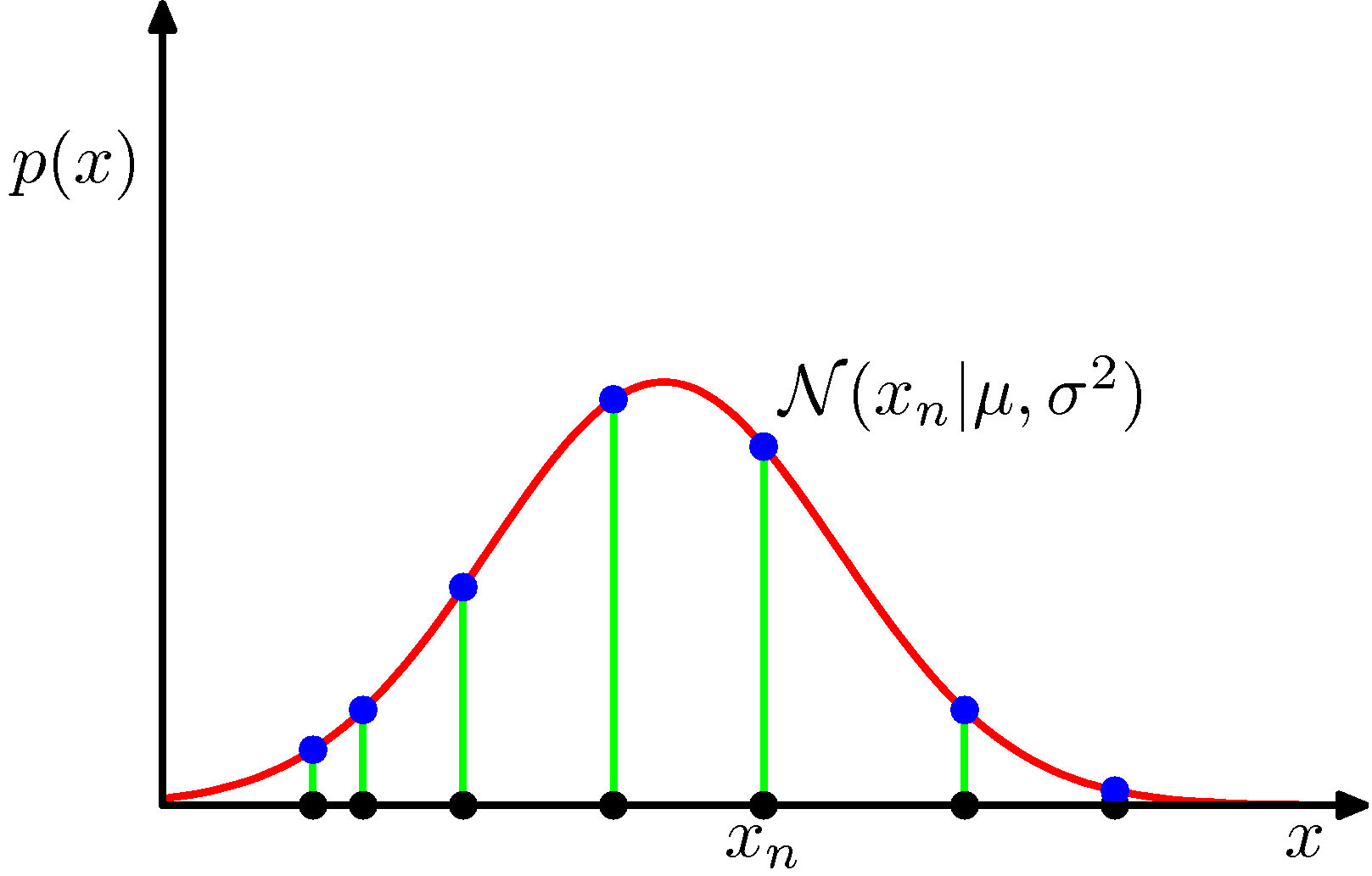
• イメージとしては、最大化することで、多くのデータが集まるところに最頻値を持ってこれる

尤度関数の最大化

$\ln p(x|\mu ,{\sigma }^2)=-\frac{1}{2{\sigma }^2}{\sum }_{n=1}^N(x_n-\mu {)}^2-\frac{N}{2}\ln {\sigma }^2-\frac{N}{2}\ln (2\pi )$

• $\mu$, $\sigma$に関して同時最大化
• 単調増加な対数をとる
  • 解析が容易になる
  • アンダーフロー防止（確率の積が和に変わる）
• 標本平均と標本分散を得る

尤度関数の最大化

• 最尤推定（Maximum Likelihood）の問題
  • 分散が過小評価される（バイアス）
  • $E\left[{\sigma }_{ML}^2\right]=\frac{N-1}{N}{\sigma }^2$
  • サンプル数が増えればバイアスも減る
  • 過学習に関連

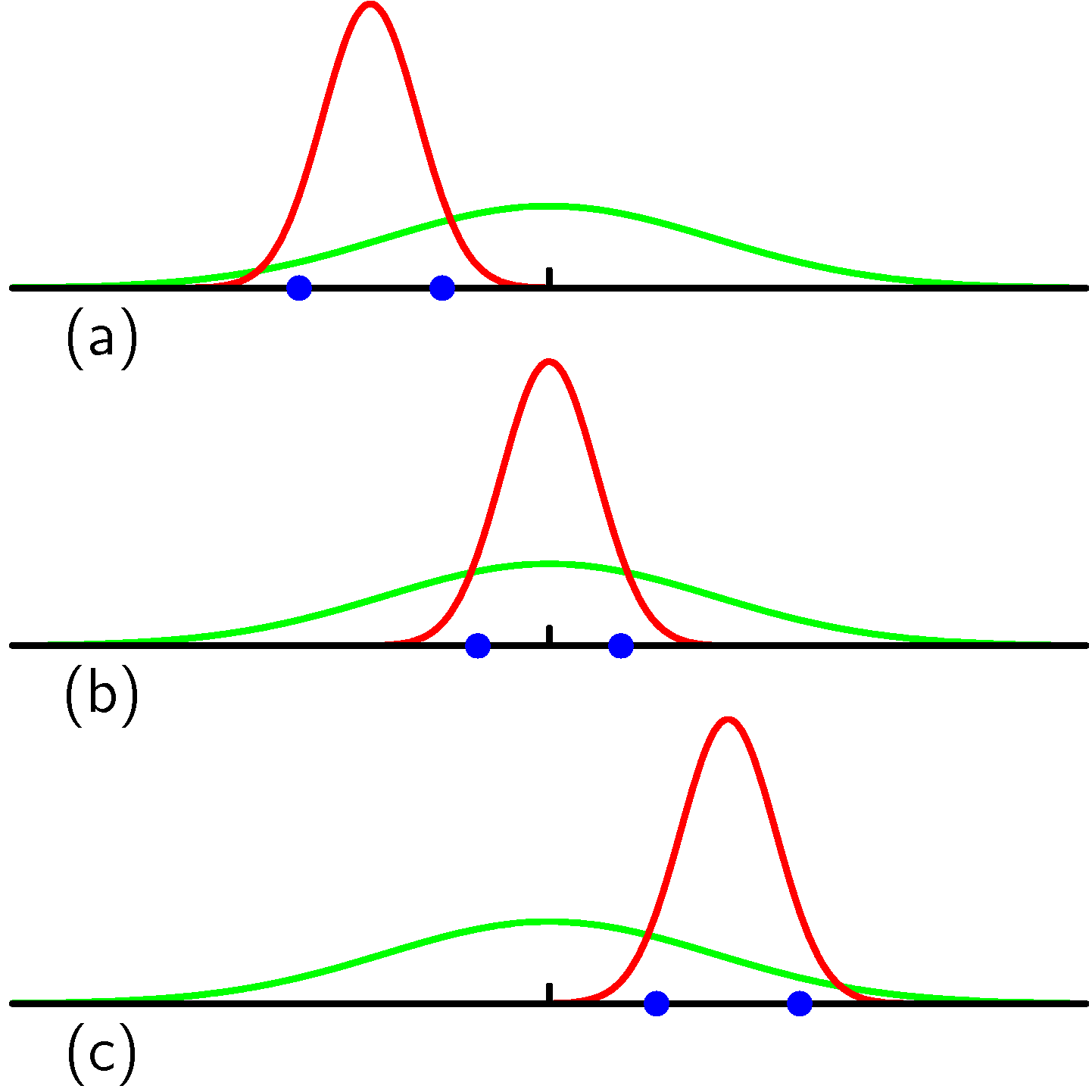
分散の過小評価の直感的説明

• 各データ集合に2点のみ
• 平均の平均は真の平均に見えるが、
• 分散はどれも $\frac{1}{2}$ に過小評価されている

分散パラメータの不偏推定量

$E\left({\sigma }_{ML}^2\right)=\frac{N-1}{N}{\sigma }^2$ より ${\tilde{\sigma }}^2=\frac{N-1}{N}{\sigma }_{ML}^2=\frac{1}{N-1}{\sum }_{n=1}N(x_n-{\mu }_{ML}{)}^2$ は分散パラメータの不偏推定量

10.1.3節で、この結果をベイズアプローチによって示す。